Setting Fair Interest Rates Based on Loss and Market Conditions
THE AUTHOR:
Naimeh Masumy, Research Fellow at Deakin University & PhD Candidate at Maastricht University
Explore our comprehensive series examining the challenges of applying statutory rates, commercial benchmarks, and compound interest in international disputes. Through case law and evolving practices, it examines how statutory rates often misalign with market realities, the uncertainty of commercial floating rates post-LIBOR, and the contentious application of compound interest with unclear doctrinal foundations.
Having established the absence of coherent guidelines in public international law and the CISG for quantifying interest, as well as the shortcomings of conflict-of-law analysis in resolving key issues—such as the divide between commercial and fixed rates, the application of compound interest, and the inconsistencies between domestic legal systems and public international law—this section outlines a method for determining a fair and reasonable rate of return. This approach, in line with UNIDROIT recommendations, aims to accurately reflect actual losses while aligning with market conditions. The objective is to ensure the rate is tailored to the specifics of each case and remains sensitive to broader market trends.
The suggested framework addresses three key issues:
- Excessive Discretion of Tribunals
Arbitral tribunals often have considerable leeway in determining interest rates. They are not strictly bound by rigid local rules or practices, and they can modify interest rates as needed within legal boundaries. Interest rates are an integral part of damage calculations and should be applied impartially, much like other procedural decisions. Accurate interest rate determination requires factual precision, especially in complex cases, and must consider factors such as inflation and associated risks.
- Limited Role of State-Mandated Regulations
Setting a realistic interest rate should minimize interference from local regulations. For example, in Middle East Comet v. Egypt, the tribunal found that applying a fixed rate didn’t account for the country’s economic instability, leading to under-compensation. Therefore, a broader view that considers the economic environment is essential.
- Problems with Relying on LIBOR
Using a single rate like LIBOR can oversimplify the process and ignore industry-specific variations. Different sectors experience unique inflation rates—industries with complex global supply chains face more volatility compared to those with localized operations. A one-size-fits-all approach can distort the true impact of interest rates on different industries.
Proposed Scheme: Investment-Based Interest Rate Determination
The proposed approach uses investment performance as the main factor in determining gains or losses, focusing on interest earnings, capital growth, associated risks, and generated income. This method, supported by Iran-U.S. claims tribunals, views investment return rates as more accurate indicators than standard commercial rates.
The suggested model takes into account several key variables of Multi-Factor Analysis for Interest Rate Adjustment:
- Varying Inflation Levels: Inflation trends differ significantly between countries.
- Industry-Specific Inflation: Each industry experiences distinct inflation patterns.
- Risk Evaluations: Different investments carry varying levels of market, credit, or country-specific risks.
This proposal prioritizes using investment return rates instead of conventional interest rate calculations. Investment disputes typically focus on a few core economic sectors, making it easier to choose a rate that aligns with the nature of the investment. Each investment has unique risks, depending on the project type.
Adjusted Compound Interest Formula
The formula adjusts the standard compound interest by factoring in inflation and risk:

So, Real Interest Rate = r – i – σ
Where:
r = Nominal interest rate
i = Inflation rate
σ = Risk premium (reflects additional risks such as market volatility or credit risks)
The formula then uses this adjusted rate in place of the nominal rate.
Understanding Rate Sensitivity
Interest rate sensitivity indicates how factors like risks and inflation affect the overall rate of return. When diverse and cumulative risks are high, the rate of return decreases. With minimal risk, the rate of return increases. Two main factors influence this sensitivity:
- Fluctuation: The extent to which inflation or other factors vary.
- Risk Premium: The additional return required to compensate for investment risks.
The essence of this proposal is to view investment performance as a primary measure for assessing damages in disputes. A review of ICSID cases shows that most disputes involve a limited set of industries, reinforcing the importance of using investment outcomes to gauge financial impacts.
The following table presents the distribution of investment tribunal disputes across five predominant industries.
An analysis of case data reveals that disputes are evenly distributed across electric power & other energy, finance, oil & gas & mining, construction, transportation, other industry, and information & communication, each accounting for approximately 14.3% of cases. These disputes primarily involve electricity distribution enterprises, renewable energy generation, banking services, mining concessions, infrastructure projects, air transportation services, and industrial manufacturing, underscoring the financial significance of investment performance in resolving such conflicts.
Assessing Risk Premium in Key Industries
The first step in the proposed formula involves integrating risk premiums to evaluate the investment’s exposure to specific risks and their potential impact on cash flow and profitability. Some investments are highly sensitive to particular risks, which can substantially influence short-term earnings and long-term value.
Steps for Accounting for Risk Premium
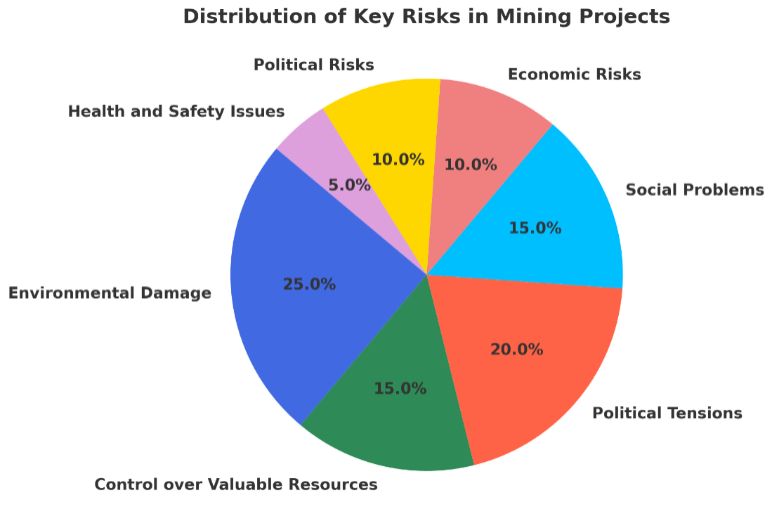
Identify Sources of Risk and Uncertainty: The first step begins by determining the types of risks that could affect performance and returns. For instance, oil and gas projects are not only capital-intensive but are also subject to heavy regulations. This makes them susceptible to government regulatory actions such as property seizures, tax disputes, or evolving environmental laws. Cases like First Majestic Silver v. Mexico (I)and Alamos Gold v. Turkeyhighlight these challenges, where changes in government policy or tax regulations undermine profitability and contractual obligations. The risks associated with such projects are illustrated in the accompanying chart.
Calculate Premium Risks Using a Risk-Adjusted Discount Rate: A Risk-Adjusted Discount Rate (“RADR”) is used to reflect risk in the determination of interest rates. This modifies the standard discount rate to reflect the risks associated with the investment, as illustrated in the following table:

Incorporating Risks into the Calculation of Interest Rates
In this mechanism, the rate adjusts for various risks affecting the compensation, such as:
- Political Risks (e.g., expropriation, regulatory changes)
- Political Tensions (foreign control of important resources)
Step 3-1 Quantify the Risk Premium:
To effectively quantify the risk premium, apply a structured method such as Probability-Weighted Risk Assessment. This involves calculating the expected impact of identified risks by combining their probabilities with potential financial outcomes. For example:
- Political Risks: Probability of regulatory changes (e.g., 30%) multiplied by the expected impact on returns (e.g., 20%).
- Political Tensions: Probability of a market downturn (e.g., 40%) multiplied by expected loss (e.g., 15%).
As showed by following formula:
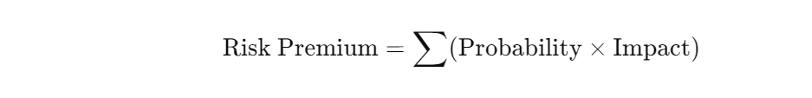
Step 3-2: Determine Base Rate:
To determine the base rate, choose an appropriate benchmark that reflects the risk-free rate or foundational interest rate. Common options include:
- Central Bank rates (e.g., Federal Reserve, ECB).
- Parties’ domestic norms risk.
Step 3-3: Incorporating Risk Premium into Calculation of Interest Rates
A risk premium represents the additional return required to compensate for risks not fully captured by the existing formula, which usually involves the use of base risks (e.g., LIBOR, SOFR, or government bond rates). This premium accounts for factors like market volatility, credit risk, country-specific risks (inflation fluctuation), and project-specific uncertainties.
To incorporate overlooked risks, such as credit risks, into the calculation of interest rates, we can use a RADR. This approach adjusts the base interest rate to reflect additional risks that affect compensation. Here’s a simplified breakdown:
The RADR formula is:
RADR= Base Rate + Risk Premium
Where:
- Base Rate: A benchmark interest rate, such as LIBOR or government bond yields.
- Risk Premium: An added percentage to reflect specific risks, such as credit risk, country risk, inflation, or project-specific risks.
Example:
- Base Interest Rate: 3% (a typical government bond rate)
- Risk Premium: A composite value calculated based on individual risks like:
- Political risk premium: 2%
- Economic risk premium: 1.5%
- Operational risk premium: 1%
- Thus, the RAIR = 3% (2% + 1,5% + 1%) = 7,5%
Benefits of Risk-Adjusted Discount Rate (“RADR”):
- Accounts for All Relevant Risks: RADR incorporates overlooked risks, such as credit, country, and project-specific risks, ensuring a more accurate reflection of the investment’s risk profile.
- Customizable for Context: RADR can be adapted to different scenarios, industries, and regions, making it versatile for arbitration and financial evaluations.
Step 3-4: Calculate the Adjusted Interest Rate:
Combine the base rate and risk premium:
Risk-Adjusted Interest Rate (“RAIR”) = Base Rate + Risk Premium
This interest rate reflects the additional risks an investor would have faced due to delays in compensation.
Applying to Compensation:
Once the RAIR is calculated, it can be applied to the principal amount owed in the compensation, using the formula:
Compensation with Interest = Principal x (1+RAIR)t
Where:
- Principal: The original amount awarded in compensation.
- RAIR: Risk-adjusted interest rate.
- t: The time in years since the injury or loss.
Example Calculation:
Let’s assume:
- Principal Compensation: $10 million
- RAIR: 7.5% (calculated above)
- Time (t): 5 years
The compensation with interest after 5 years at a 7.5% risk-adjusted interest rate is $14,356,290. This includes the original $10 million in compensation and $4,356,290 accrued as interest over the 5-year period, after incorporating risks.
Accounting for Inflation
Inflation significantly impacts both nominal interest rates and the purchasing power of future cash flows from investments; therefore, it is a crucial element in accurately calculating interest rates. However, inflation shows considerable variation across the Organisation for Economic Co-operation and Development (“OECD”), G7, eurozone, and G20 countries.
Overall, inflation has declined, with OECD inflation falling to 5.6% in June 2024, the lowest level since October 2021. However, not all countries experienced such a steady decline. While headline inflation has decreased in many countries, there are stark contrasts; some countries, such as Turkey, face inflation rates exceeding 70%, while others in the eurozone see much lower rates.
The varied inflation rates can be primarily attributed to differing fiscal policies, supply-side shocks, localized labor conditions, and global supply chains. Typically, countries experiencing political instability, corruption, or economic crises tend to have much higher inflation rates due to a collapse in market confidence, currency devaluation, and limited control over monetary policy. For example, Zimbabwe has faced inflationary crises for over a decade due to government mismanagement, political instability, and agricultural disruptions. Similarly, Venezuela’s inflation remains relatively high, with the International Monetary Fund (“IMF”) estimating it at 250% for this year. Argentina’s ongoing inflation crisis reached 124% in 2023, driven by excessive public spending, high debt, and a move away from the local currency. Countries reliant on energy imports, especially oil and gas, are more vulnerable to fluctuations in global energy prices.
In parallel, nations that depend heavily on imports may experience inflation when global supply chains are disrupted or tariffs are imposed. For instance, during the COVID-19 pandemic, supply chain disruptions led to higher inflation in many industrialized countries. In contrast, developed economies with stable growth and diversified industries tend to experience lower and more controlled inflation. In the euro area, inflation remained stable, hovering between 2.4% and 2.9%, with some countries like Lithuania and Finland reporting headline inflation rates below 1.0%. In contrast, G20 inflation remained higher, particularly in Argentina, where it exceeded 270%, and Brazil, where inflation rose for consecutive months. Energy prices also serve as a critical component of overall inflation. While countries like Turkey and Colombia saw energy prices rise by more than 10%, others, such as the UK and Sweden, experienced significant declines in energy costs.
With inflationary pressures differing significantly across countries and their unique economic conditions, the demand for tailored inflation adjustments has become increasingly essential.
Adjusting for Inflation Volatility
In a global context where states experience varied inflation rates, adjustments can be made based on internal market trends over the duration of an investment. The one-size-fits-all model, which assumes general market trends while disregarding individual inflation rates, renders existing calculation methods erroneous and fundamentally flawed.
The eschewed interaction between inflation rate and interest rates can be expressed using the Fisher equation. This equation links the nominal interest rate with the real interest rate and inflation.
The following is a step-by-step approach to endorsing the Fisher equation to first account for inflation in the nominal interest rate and then incorporating that into the compound interest formula which encompasses risk premium.
Step 1: Fisher Equation to Account for Inflation
The Fisher equation focuses solely on the relationship between the nominal interest rate, the real interest rate, and inflation. It is used to strike a coherent balance between inflation rate and nominal interest.
The Fisher equation without the risk premium is given by: i = r + π
Where:
- i is the nominal interest rate
- r is the real interest rate (the return or cost excluding inflation)
- π is the expected inflation rate
Using the equation:
i = r + πi
And substituting the given values:
i = 0.03 + 0.04 = 0.07 or 7%
Thus, the nominal interest rate is 7%, which includes a real return of 3% and an expected inflation rate of 4%. This means that in this scenario, the stated interest rate on investments accounts for both the real return and anticipated inflation, ensuring an accurate measure of investment performance.
Interpretation
- The real interest rate of 3% represents the actual purchasing power gain from the investment or loan.
- The 4% expected inflation reflects how much the currency is expected to lose value over time.
- The nominal interest rate of 7% is the total rate, which accounts for both the real return and the expected inflation.
Step 2: Incorporate Risk Premium into the Compound Interest Formula
The adjusted compound interest formula accounts for inflation and real return through the nominal interest rate, calculated using the Fisher equation. After determining the nominal rate, a risk premium(“RP”) is added separately to account for specific risks such as credit, country, or project risks, ensuring a more accurate reflection of investment returns.
The compound interest formula becomes:
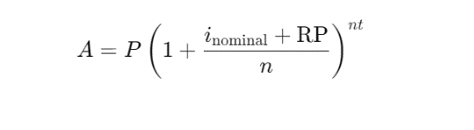
Where:
- A is the future value,
- P is the principal,
- inominal is the nominal interest rate calculated using the Fisher equation,
- RP is the risk premium (accounting for risks like default, liquidity, or credit risk),
- n is the number of compounding periods per year,
- t is the time in years.
Example Calculation
Let’s assume:
- Real interest rate (r): 3% (or 0.03),
- Expected inflation rate (π): 4% (or 0.04),
- Risk premium (RP): 2% (or 0.02),
- Principal (P): $1,000,
- Interest compounded quarterly (n = 4),
- Time (t = 5) years.
Step 3: Adjust for Inflation to Find the Real Value
Calculate the real value, adjusted for inflation.
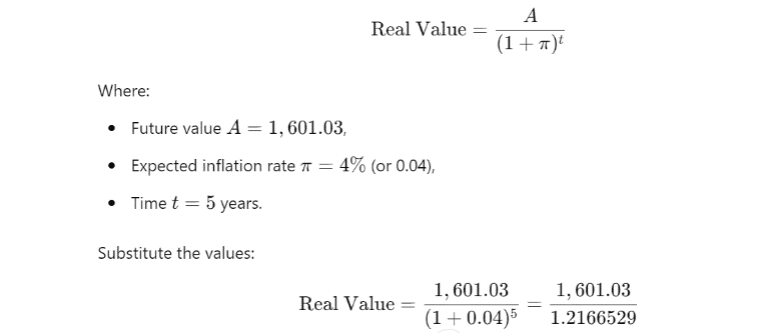
Calculate the Nominal Interest Rate Using Fisher Equation
First: The nominal interest rate is determined using the Fisher Equation, which connects the real interest rate, expected inflation rate, and nominal interest rate.
Step 1: Calculate the Nominal Interest Rate
The Nominal Interest Rate is calculated using the Fisher Equation to incorporate:
- Real Interest Rate: The actual growth or return excluding inflation.
- Inflation Rate: The expected change in purchasing power over time.
The Fisher Equation is shown below:
(1+Nominal Interest Rate)= (1+Real Interest Rate) × (1+Inflation Rate)
inominal = r + π = 0.03 + 0.04 = 0.07 or 7%
Step 2: Add the Risk Premium
Once the Nominal Interest Rate is calculated, a Risk Premium is added to adjust for case-specific risks (e.g., country risk, credit risk, or project-specific risks). This results in the Risk-Adjusted Interest Rate (“RAIR”):
RAIR= Nominal Interest Rate+ Risk Premium
Step 3: Use the Compound Interest Formula
Apply the Risk-Adjusted Interest Rate in the compound interest formula to calculate compensation with interest:
Compensation with Interest= Principal × (1+RAIR)^t
Where:
- Principal: The original compensation amount.
- RAIR: The combined rate, including nominal interest and risk premium.
- t: The time period (in years).
Example:
Inputs:
- Principal Compensation: $10 million
- Real Interest Rate: 3%
- Inflation Rate: 4%
- Risk Premium: 2.5%
- Time Period (t): 5 years
Step 1: Calculate the Nominal Interest Rate
(1+Nominal Interest Rate)= (1+0.03)×(1+0.04) =1.03×1.04=1.0712
Nominal Interest Rate= 1.0712−1=0.0712 or 7.12%
Step 2: Add the Risk Premium
RAIR=7.12%+2.5%=9.62% or 0.0962
Step 3: Calculate Compensation with Interest
Compensation with Interest=10,000,000×(1+0.0962)^5
Compensation with Interest=10,000,000×(1.0962)^5=10,000,000×1.5728=15,728,000
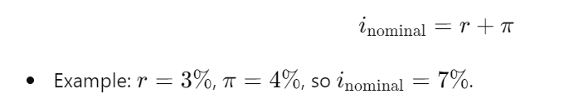
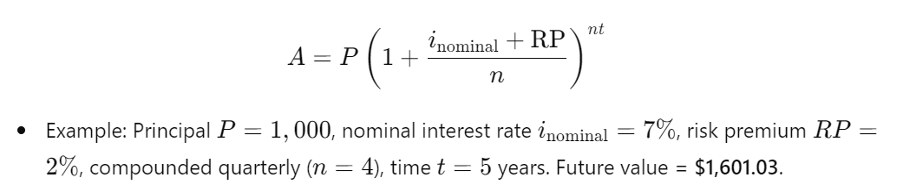
The key benefits of this formula:
- Separation of risk premium and Inflation rate:
- Fisher Equation Focuses on Economic Fundamentals: By using the Fisher equation solely to account for the real interest rate and inflation, the formula provides a clear picture of how inflation impacts the rate of return.
- Risk Premium is Separate: Keeping the risk premium separate in the compound interest formula allows for a more detailed breakdown of how various risks—such as expropriation risks, environmental risks, and socio-political hazards—affect the rate of interest.
- Flexibility in Adjusting for Different Types of Risks
- Customizable Risk Premiums: The formula allows flexibility by enabling you to add specific risk premiums for different investments or financial instruments.
- Granular Risk Analysis: By separating the risk premium, you can analyze which specific risks (e.g., economic risk, oil and gas related hazards, or liquidity risk) contribute to the higher interest rates, and fine-tune your risk management strategies accordingly.
- Better Insight into Real vs. Nominal Returns
- Transparent View of Nominal Interest Rate: The formula offers a transparent breakdown of how much of the nominal interest rate is driven by the real return and inflation, and how much is attributed to risk premiums.
- Accurate Calculation of Real Value: Since the risk premium is kept separate, you can accurately calculate the real value (adjusted for inflation) of future amounts without conflating the risk premium.
ABOUT THE AUTHOR
Naimeh Masumy is a PhD Candidate at Maastricht University and a Research Fellow at Deakin University. In her professional capacity, she advises on international trade, regulatory compliance, and arbitration under ICC and UNCITRAL rules. Naimeh serves on the International Transnational Arbitration Advisory Board and the editorial board of ITA in Review. She holds an LLM in international banking and finance law from University College London and a degree in international legal studies from the University of Pennsylvania.
*The views and opinions expressed by authors are theirs and do not necessarily reflect those of their organizations, employers, or Daily Jus, Jus Mundi, or Jus Connect.





